Dancing Links (DLX 算法)学习笔记

xxy 收录于类别杂记随想

2021-09-22 2021-09-22 约 4037 字预计阅读 9 分钟次阅读条评论

https://cdn.jsdelivr.net/gh/xxy-im/storage@gh-pages/images/dancinglinks.png

计算机程序设计艺术，第四卷第五册C，Dancing Links(舞蹈链算法)

Dancing Links (舞蹈链)，是大名鼎鼎的 高德纳(Donald Knuth) 为快速实现他提出的X算法所提出的一种数据结构，所以也叫做 DLX算法，其目的是用于解决 精确覆盖问题。

覆盖问题

集合$S = \lbrace1, 2, 3, 4, 5, 6, 7\rbrace$，有其子集
$S_1 = \lbrace3, 5\rbrace$
$S_2 = \lbrace1, 4, 7\rbrace$
$S_3 = \lbrace2, 3, 6\rbrace$
$S_4 = \lbrace1, 4, 6\rbrace$
$S_5 = \lbrace2, 7\rbrace$
$S_6 = \lbrace4, 5, 7\rbrace$

选择一些子集组成集合 $T$ ，使得 $T$ 中的包含的元素能覆盖集合 $S$ ，即 $S$ 中的所有元素都能在 $T$ 中找到包含它的子集（$\forall x \in S \rightarrow \forall x \in T$）。

重复覆盖： 集合 $S$ 中的任意成员 $x$ 允许同时属于两个以上的子集，例如 $T=\lbrace S_1, S_2, S_3\rbrace$ 重复覆盖S。
精确覆盖： 集合 $S$ 中的任意成员 $x$ 属于且只属于 $T$ 中的一个子集，例如 $T=\lbrace S_1, S_4, S_5\rbrace$ 精确覆盖S。

用矩阵表示上述问题：

算法步骤如下：

如果矩阵 $A$ 为空且所有列都被选中，则当前局部解即为问题的一个解，返回成功；否则继续。

根据一定方法选择第 $c$ 列。如果某一列中没有1，则返回失败，并去除当前局部解中最新加入的行。

选择第 $r$ 行，使得 $A_{(r,c)} = 1$（该步是不确定的）。

将第 $r$ 行加入当前局部解中。

对于满足 $A_{(r,j)} = 1$ 的每一列 $j$，从矩阵 $A$ 中删除所有满足$A_{(i,j)} = 1$的行，最后再删除第 $j$ 列。

对所得比 $A$ 小的新矩阵递归地执行此算法。 $$ %S = % \begin{pmatrix} % 0 & 0 & 1 & 0 & 1 & 0 & 0\\ % 1 & 0 & 0 & 1 & 0 & 0 & 1\\ % 0 & 1 & 1 & 0 & 0 & 1 & 0\\ % 1 & 0 & 0 & 1 & 0 & 1 & 0\\ % 0 & 1 & 0 & 0 & 0 & 0 & 1\\ % 0 & 0 & 0 & 1 & 1 & 0 & 1\\ % \end{pmatrix} $$

即选出矩阵的若干行，使得其中的1在所有列中出现且仅出现一次
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} & \mathbf{5} & \mathbf{6} & \mathbf{7}\\ \hline \mathbf{\textcolor{blue}{S_1}} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{1} & \textcolor{blue}{0} & \textcolor{blue}{1} & \textcolor{blue}{0} & \textcolor{blue}{0}\\ \hline \mathbf{S_2} & 1 & 0 & 0 & 1 & 0 & 0 & 1\\ \hline \mathbf{S_3} & 0 & 1 & 1 & 0 & 0 & 1 & 0\\ \hline \mathbf{\textcolor{blue}{S_4}} & \textcolor{blue}{1} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{1} & \textcolor{blue}{0} & \textcolor{blue}{1} & \textcolor{blue}{0}\\ \hline \mathbf{\textcolor{blue}{S_5}} & \textcolor{blue}{0} & \textcolor{blue}{1} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{1}\\ \hline \mathbf{S_6} & 0 & 0 & 0 & 1 & 1 & 0 & 1\\ \hline \end{array} $$ 蓝色标记的三行($S_1, S_4, S_5$)，便是精确覆盖问题的解 $$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} & \mathbf{5} & \mathbf{6} & \mathbf{7}\\ \hline \mathbf{\textcolor{blue}{S_1}} & \textcolor{blue}{0} & \textcolor{blue}{0} & \fcolorbox{red}{aqua}{1} & \textcolor{blue}{0} & \fcolorbox{red}{aqua}{1} & \textcolor{blue}{0} & \textcolor{blue}{0}\\ \mathbf{\textcolor{blue}{S_4}} & \fcolorbox{red}{aqua}{1} & \textcolor{blue}{0} & \textcolor{blue}{0} & \fcolorbox{red}{aqua}{1} & \textcolor{blue}{0} & \fcolorbox{red}{aqua}{1} & \textcolor{blue}{0}\\ \mathbf{\textcolor{blue}{S_5}} & \textcolor{blue}{0} & \fcolorbox{red}{aqua}{1} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} & \fcolorbox{red}{aqua}{1}\\ \hline \end{array} $$
肉眼很容易一眼看出答案，但是计算机需要具体的算法步骤才行。下面看看 X算法 是如何求解的。

X算法（DFS回溯）

初始状态： $$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} & \mathbf{5} & \mathbf{6} & \mathbf{7}\\ \hline \mathbf{S_1} & 0 & 0 & 1 & 0 & 1 & 0 & 0\\ \hline \mathbf{S_2} & 1 & 0 & 0 & 1 & 0 & 0 & 1\\ \hline \mathbf{S_3} & 0 & 1 & 1 & 0 & 0 & 1 & 0\\ \hline \mathbf{S_4} & 1 & 0 & 0 & 1 & 0 & 1 & 0\\ \hline \mathbf{S_5} & 0 & 1 & 0 & 0 & 0 & 0 & 1\\ \hline \mathbf{S_6} & 0 & 0 & 0 & 1 & 1 & 0 & 1\\ \hline \end{array} $$

高德纳建议每次选取 1 最少的列

X算法的执行步骤如下：
第一步：
选取1最少的列，此时第1，2，3，5，6列1的个数都是2，选择第1列。第1列中 $S_2$ 和 $S_4$均为1，选择 $S_2$ 加入当前解。（$T=\lbrace S_2\rbrace$）
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & \mathbf{\textcolor{blue}{1}} & \mathbf{2} & \mathbf{3} & \mathbf{\textcolor{blue}{4}} & \mathbf{5} & \mathbf{6} & \mathbf{\textcolor{blue}{7}}\\ \hline \mathbf{S_1} & 0 & 0 & 1 & 0 & 1 & 0 & 0\\ \hline \mathbf{\textcolor{blue}{S_2}} & \textcolor{blue}{1} & 0 & 0 & \textcolor{blue}{1} & 0 & 0 & \textcolor{blue}{1}\\ \hline \mathbf{S_3} & 0 & 1 & 1 & 0 & 0 & 1 & 0\\ \hline \mathbf{S_4} & 1 & 0 & 0 & 1 & 0 & 1 & 0\\ \hline \mathbf{S_5} & 0 & 1 & 0 & 0 & 0 & 0 & 1\\ \hline \mathbf{S_6} & 0 & 0 & 0 & 1 & 1 & 0 & 1\\ \hline \end{array} $$

第二步：
第1列中$S_2$行和$S_4$行为1，第4列中$S_2$，$S_4$和$S_6$行为1，第7列中$S_2$，$S_5$和$S_6$行为1。所以移除第1，4，7列和$S_2$，$S_4$，$S_5$，$S_6$行。
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & \mathbf{\textcolor{blue}{1}} & \mathbf{2} & \mathbf{3} & \mathbf{\textcolor{blue}{4}} & \mathbf{5} & \mathbf{6} & \mathbf{\textcolor{blue}{7}}\\ \hline \mathbf{S_1} & \textcolor{blue}0 & 0 & 1 & \textcolor{blue}0 & 1 & 0 & \textcolor{blue}0\\ \hline \mathbf{\textcolor{blue}{S_2}} & \textcolor{blue}{1} & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}{1} & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}{1}\\ \hline \mathbf{S_3} & \textcolor{blue}0 & 1 & 1 & \textcolor{blue}0 & 0 & 1 & \textcolor{blue}0\\ \hline \mathbf{\textcolor{blue}{S_4}} & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}0\\ \hline \mathbf{\textcolor{blue}{S_5}} & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}1\\ \hline \mathbf{\textcolor{blue}{S_6}} & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}1\\ \hline \end{array} $$ 第三步：
此时只剩下了$S_1$和$S_3$行可选，矩阵非空，算法继续执行递归回到第一步，此时初始状态如下。
$$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{2} & \mathbf{3} & \mathbf{5} & \mathbf{6} \\ \hline \mathbf{S_1} & 0 & 1 & 1 & 0\\ \hline \mathbf{S_3} & 1 & 1 & 0 & 1\\ \hline \end{array} $$

第一步：
此时第2，5，6列1的个数最少，选取第2列，即将对应的 $S_3$ 加入当前解。
（$T=\lbrace S_2, S_3 \rbrace$）
$$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{\textcolor{blue}{2}} & \mathbf{\textcolor{blue}{3}}& \mathbf{5} & \mathbf{\textcolor{blue}{6}} \\ \hline \mathbf{S_1} & 0 & 1 & 1 & 0\\ \hline \mathbf{\textcolor{blue}{S_3}} & \textcolor{blue}1 & \textcolor{blue}1 & 0 & \textcolor{blue}1\\ \hline \end{array} $$
第二步：
移除 $S_3$ 关联的行列。 $$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{\textcolor{blue}{2}} & \mathbf{\textcolor{blue}{3}} & \mathbf{5} & \mathbf{\textcolor{blue}{6}} \\ \hline \mathbf{\textcolor{blue}{S_1}} & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}0\\ \hline \mathbf{\textcolor{blue}{S_3}} & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}1\\ \hline \end{array} $$
第三步：
矩阵为空，但是第5列仍没被选择，所以求解失败，需要回溯到新的行加入解集之前一步，并作另一选择再次执行算法。 $$ \begin{array}{|c|} \hline \mathbf{5}\\ \hline \end{array} $$

回溯： $$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{2} & \mathbf{3} & \mathbf{5} & \mathbf{6} \\ \hline \mathbf{S_1} & 0 & 1 & 1 & 0\\ \hline \mathbf{S_3} & 1 & 1 & 0 & 1\\ \hline \end{array} $$ 第一步：
因为之前在这一步选择了 $S_3$，所以这次我们选择 $S_1$ 加入局部最优解，即（$T=\lbrace S_1, S_2 \rbrace$）。
$$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{2} & \mathbf{\textcolor{blue}{3}} & \mathbf{\textcolor{blue}{5}} & \mathbf{6} \\ \hline \mathbf{\textcolor{blue}{S_1}} & 0 & \textcolor{blue}1 & \textcolor{blue}1 & 0\\ \hline \mathbf{S_3} & 1 & 1 & 0 & 1\\ \hline \end{array} $$
第二步：
移除 $S_1$ 关联的行列。 $$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{2} & \mathbf{\textcolor{blue}{3}} & \mathbf{\textcolor{blue}{5}} & \mathbf{6} \\ \hline \mathbf{\textcolor{blue}{S_1}} & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}0\\ \hline \mathbf{\textcolor{blue}{S_3}} & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}1\\ \hline \end{array} $$
第三步：
矩阵为空，但还有第2，6列未被选中，所以需要再次回溯，此时需要再往上一次回溯了，即回到了矩阵最初始状态。 $$ \begin{array}{|c|c|} \hline \mathbf{2} & \mathbf{6} \\ \hline \end{array} $$
再次回溯：
回到了最初始状态。 $$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} & \mathbf{5} & \mathbf{6} & \mathbf{7}\\ \hline \mathbf{S_1} & 0 & 0 & 1 & 0 & 1 & 0 & 0\\ \hline \mathbf{S_2} & 1 & 0 & 0 & 1 & 0 & 0 & 1\\ \hline \mathbf{S_3} & 0 & 1 & 1 & 0 & 0 & 1 & 0\\ \hline \mathbf{S_4} & 1 & 0 & 0 & 1 & 0 & 1 & 0\\ \hline \mathbf{S_5} & 0 & 1 & 0 & 0 & 0 & 0 & 1\\ \hline \mathbf{S_6} & 0 & 0 & 0 & 1 & 1 & 0 & 1\\ \hline \end{array} $$

第一步：
前面第一次选择了 $S_2$，所以这次选择将 $S_4$ 加入局部最优解。（$T=\lbrace S_4 \rbrace$）
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & \mathbf{\textcolor{blue}{1}} & \mathbf{2} & \mathbf{3} & \mathbf{\textcolor{blue}{4}} & \mathbf{5} & \mathbf{\textcolor{blue}{6}} & \mathbf{7}\\ \hline \mathbf{S_1} & 0 & 0 & 1 & 0 & 1 & 0 & 0\\ \hline \mathbf{S_2} & 1 & 0 & 0 & 1 & 0 & 0 & 1\\ \hline \mathbf{S_3} & 0 & 1 & 1 & 0 & 0 & 1 & 0\\ \hline \mathbf{\textcolor{blue}{S_4}} & \textcolor{blue}1 & 0 & 0 & \textcolor{blue}1 & 0 & \textcolor{blue}1 & 0\\ \hline \mathbf{S_5} & 0 & 1 & 0 & 0 & 0 & 0 & 1\\ \hline \mathbf{S_6} & 0 & 0 & 0 & 1 & 1 & 0 & 1\\ \hline \end{array} $$

第二步： 移除 $S_4$ 关联的行列。 $$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & \mathbf{\textcolor{blue}{1}} & \mathbf{2} & \mathbf{3} & \mathbf{\textcolor{blue}{4}} & \mathbf{5} & \mathbf{\textcolor{blue}{6}} & \mathbf{7}\\ \hline \mathbf{S_1} & \textcolor{blue}0 & 0 & 1 & \textcolor{blue}0 & 1 & 0 & 0\\ \hline \mathbf{\textcolor{blue}{S_2}} & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}1\\ \hline \mathbf{S_3} & \textcolor{blue}0 & 1 & 1 & \textcolor{blue}0 & 0 & 1 & 0\\ \hline \mathbf{\textcolor{blue}{S_4}} & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}0\\ \hline \mathbf{S_5} & \textcolor{blue}0 & 1 & 0 & \textcolor{blue}0 & 0 & 0 & 1\\ \hline \mathbf{\textcolor{blue}{S_6}} & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}1\\ \hline \end{array} $$

第三步：
矩阵非空，递归回到第一步 $$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{2} & \mathbf{3} & \mathbf{5} & \mathbf{7}\\ \hline \mathbf{S_1} & 0 & 1 & 1 & 0\\ \hline \mathbf{S_3} & 1 & 1 & 0 & 0\\ \hline \mathbf{S_5} & 1 & 0 & 0 & 1\\ \hline \end{array} $$

第一步：
第5列1最少，选择 $S_1$ 加入局部最优解。（$T=\lbrace S_2, S_4 \rbrace$）
$$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{2} & \mathbf{3} & \mathbf{5} & \mathbf{7}\\ \hline \mathbf{S_1} & 0 & \textcolor{blue}1 & \textcolor{blue}1 & 0\\ \hline \mathbf{S_3} & 1 & 1 & 0 & 0\\ \hline \mathbf{S_5} & 1 & 0 & 0 & 1\\ \hline \end{array} $$

第二步：
移除 $S_1$关联的行列。 $$ \begin{array}{|c|c|c|c|c|} \hline & \mathbf{2} & \mathbf{\textcolor{blue}{3}} & \mathbf{\textcolor{blue}{5}} & \mathbf{7}\\ \hline \mathbf{\textcolor{blue}{S_1}} & \textcolor{blue}0 & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}0\\ \hline \mathbf{\textcolor{blue}{S_3}} & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}0 & \textcolor{blue}0\\ \hline \mathbf{S_5} & 1 & \textcolor{blue}0 & \textcolor{blue}0 & 1\\ \hline \end{array} $$

第三步：
矩阵非空且无全0列，将最后一行加入局部最优解。（$T=\lbrace S_2, S_4, S_5 \rbrace$）
$$ \begin{array}{|c|c|c|} \hline & \mathbf{2} & \mathbf{7}\\ \hline \mathbf{S_5} & 1 & 1\\ \hline \end{array} $$
第四步：
此时矩阵为空，且所有列均被选中。求解成功，最终解为 $T=\lbrace S_2, S_4, S_5 \rbrace$，与肉眼观察法得出的答案一致。

Dancing Links

上述回溯求解过程存在大量的缓存矩阵和回溯矩阵的过程。而简单DFS回溯在这些过程中需要不断的删除又创建矩阵，当递归深度过深时还有可能栈溢出。于是算法大师高德纳提出了DLX(Dancing Links X)算法，即使用 Dancing Links 这一数据结构实现X算法。使得整个回溯算法过程中只需要使用一个矩阵链。算法执行过程中，指针在数据之间跳跃着，就像精巧设计的舞蹈一样，故称之为 Dancing Links (舞蹈链)。

舞蹈链的核心是双向链表实现的，先来看看双向链表的删除和插入操作。

https://cdn.jsdelivr.net/gh/xxy-im/storage@gh-pages/images/doublelinks.png — 双向链表

双向链表中任一元素都能很容易得到它左右两边（Left和Right指针）的元素。

删除Col2：

1
2
3
4


Col1.Right = Col3;
Col3.Left = Col1;

// delete Col2;

此时我们并没有真的将Col2删除，只是链表遍历不到它了
插入Col2：

1
2


Col1.Right = Col2;
Col3.Left = Col2;

可以看出上面删除和插入都是 $O(1)$ 的。仔细想想这两个操作是不是和算法过程中的缓存，回溯对应。所以我们可以用链表的删除和插入来代替回溯算法中的缓存和回溯过程，且不需要开辟新的内存空间。

数据结构定义

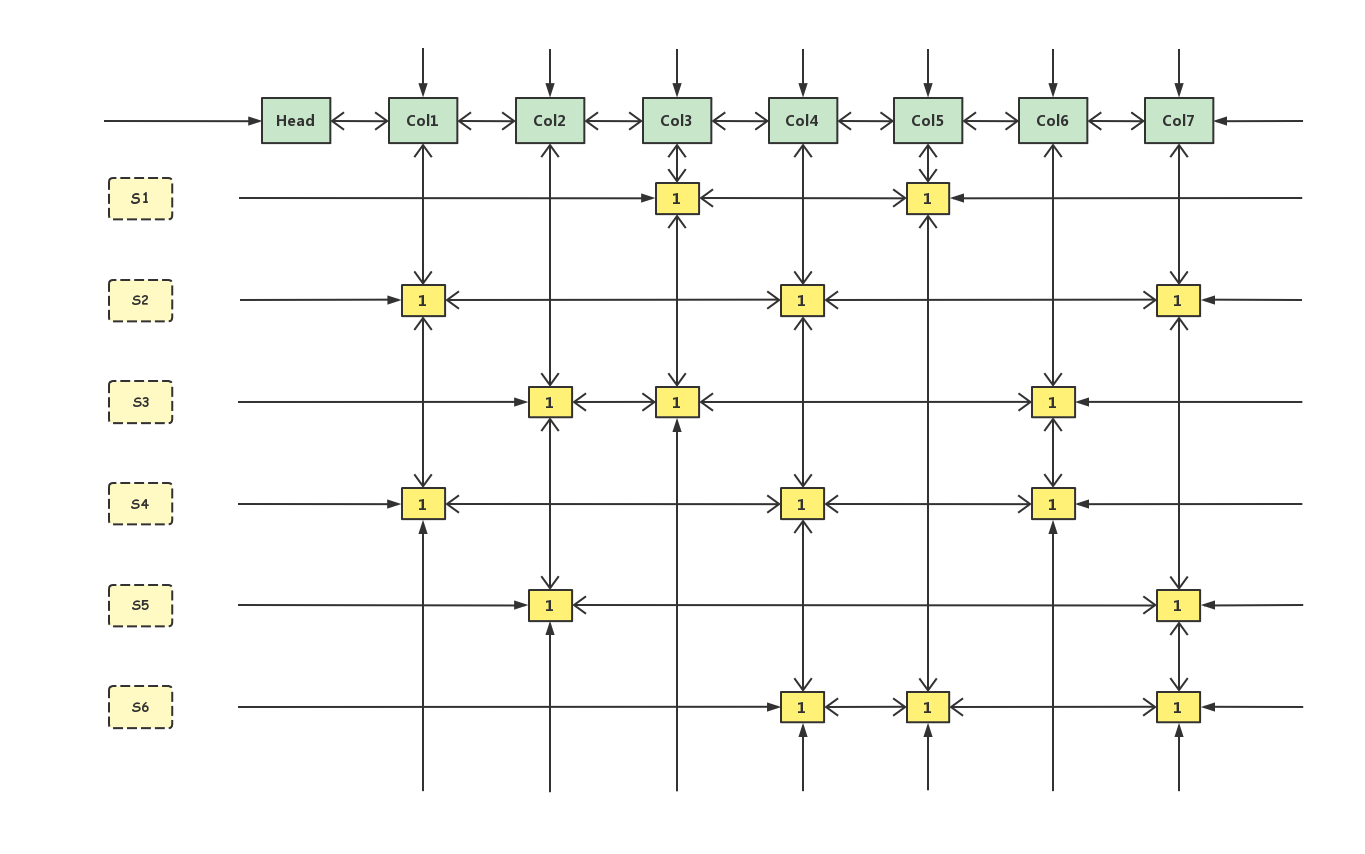
Dancing Links使用的是十字交叉双向循坏列表，即每个结点除了 Left, Right 指针外还存在 Up, Down 指针。同时还有一个指针指向所在的列结点。还需要一个Head结点，当Head->Right == Head 为 true 时，求解结束。（Head 结点只有 Left, Right 两个有效指针）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


class DLNode
{
public:
  DLNode * Left;           // 左结点
  DLNode *Right;          // 右结点
  DLNode *Up;             // 上结点
  DLNode *Down;           // 下结点
  DLNode *Col;            // 所属列结点
  
  int row;                // 行号
  int nums;               // 该列存在的结点个数（当结点为列结点时有效，否则为-1）
  
  DLNode(DLNode *Col, int n, int s = -1):   
      Left(this), Right(this), Up(this), Down(this), 
      Col(Col), row(n), nums(s){ if (Col) Col->Add2Colume(this); };
  ~DLNode() {};
  
  void Add2Row(DLNode *node);            // 添加结点到该行末尾
  void Add2Colume(DLNode *node);         // 添加结点到该列尾
  
  void RemoveCol();                      // 移除该结点所在的列
  void RecoverCol();                     // 还原列
  void Remove();                         // 移除该结点关联的行和列
};
  
class DancingLinks
{
public:
  DancingLinks(int s[M][N]);
  ~DancingLinks();
  
  DLNode *Head;                   // 头结点
  std::vector<DLNode *> Cols;     // 列向量
  std::vector<DLNode *> Ans;      // 保存结果
  
  bool DLX();                     // DLX算法求解
  void ShowResult();              // 输出结果
};

根据前面的精确覆盖问题构建Dancing Links结构。

https://cdn.jsdelivr.net/gh/xxy-im/storage@gh-pages/images/dl-struct.png — Dancing Links结构图

DLX算法求解过程

首先判断 Head->Right == Head，若为真，求解完成，输出结果。否则算法继续执行。执行过程与前面所述的X算法类似，因此不再赘述。
代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87


// 初始化Dancing Links
DancingLinks::DancingLinks(int s[M][N])
{
    Head = new DLNode(nullptr, 0);

    // N列，创建N个列结点
    for (int i = 0; i < N; i++)
    {
      auto t = new DLNode(nullptr, 0, 0);
      Head->Add2Row(t);
      Cols.push_back(t);
    }

    for (int r = 0; r < M; r++)
    {
        bool flag = false;
        DLNode *node = nullptr;
        for (int c = 0; c < N; c++)
        {
            // 创建结点
            if (s[r][c])
            {
                // 该行的第一个结点
                if (!flag)
                {
                    node = new DLNode(Cols[c], r+1);
                    flag = true;
                }

                node->Add2Row(new DLNode(Cols[c], r+1));
            }
        }
    }

    // 移除初始为空的列
    for (auto col = Head->Right; col != Head; col = col->Right)
	{
		if (!col->nums) col->RemoveCol();
	}
}

// DLX算法
bool DancingLinks::DLX()
{
    if (Head->Right == Head)
	{
		ShowResult();
		return true;
	}

    DLNode *col = nullptr;
	int min = INT_MIN;

    // 找到列元素最少的列
	for (auto c = Head->Right; c != Head; c = c->Right)
	{
		if (min > c->nums)
		{
			col = c;
			min = c->nums;
		}
	}

    col->RemoveCol();

	for (auto node = col->Down; node != col; node = node->Down)
	{
		Ans.push_back(node);

		for (auto rnode = node->Right; rnode != node; rnode = rnode->Right)
		{
			rnode->Col->RemoveCol();
		}

		if (DLX())
            return true;

		for (auto lnode = node->Left; lnode != node; lnode = lnode->Left)
		{
			lnode->Col->RecoverCol();
		}

		Ans.pop_back();
	}

	col->RecoverCol();
}

程序完整代码：
https://github.com/xxy-im/DancingLinks

参考文章

https://en.wikipedia.org/wiki/Dancing_Links
https://www.cnblogs.com/grenet/p/3163550.html

目录